

This the first of a series of articles presenting solutions to the following business problem:
Today's AI innovation is enabled by a rapidly falling cost of number crunching per dollar. Yet computational resources are never unlimited, and can sometimes be quite constrained. AI innovation is also being driven by rapidly falling cost of data acquisiton. Places of data acquisition are becoming so critical that they now have their own buzzword: the edge. At the edge, it's not always practical to bring heavy computational burden. It's easy for sensors like high end video to saturate the networks you have available. And in the day of GDPR, privacy requirements may make shipping raw data to the cloud untenable.
Here's our scenario: Your business seeks to make predictions on edge devices that need to be small, inexpensive, or low power. You can use as much computation as needed to build your model in the cloud. However at the edge, the device needs to make predictions on its own, without the luxury of heavy computation. Frugality in computation is required to make your data collection and prediction work together.
This article shares experience learned in using books, papers and open source code to create real working systems.
In practice, book formulas are frequently challenging to turn into code. In practice, open source code often crashes. Both kinds of concrete difficulties will be shared in the course of this article.
We will not assume prior knowledge of deep learning. We will assume familiarity with python and basic calculus.
A deep learning AI model is a list of large formulas with numeric blanks to be filled in. The formula list is called a network. The formulas are called network nodes. The blanks are called parameters.
When a parameter is nonzero, it represents a connection in the network. When a parameter is zero, it represents a disconnection in the network, and typically computational work can be skipped at prediction time. The more zero parameters we have, the more work we can skip.
The fraction of the parameters that are nonzero is known as model sparsity.
This article's approach to edge device efficiency will be to train models that have efficiency built-in through model sparsity.
Processing models after training also presents opportunities for computational savings. For a good list of post-training computational efficiency improvements, consult the Tensorflow Lite User Guide. Any of those techniques can be used in addition to training with model sparsity.
Applying regularization to our model will direct model training to search for sparse model solutions, solutions with more zero weights. For each weight equal to zero, scoring can be skipped, lowering the footprint of scoring on your edge device.
The remainder of this article will have three parts. First, we will talk about how books say regularization works. Second, we will try two different Tensorflow APIs for regularization. Finally, we will learn what the better Tensorflow API does and use our knowledge to build more flexible implementation of regularization.
The github repository Using_L1_Regularization provides all code in this article, and instructions on how to set it up.
We discuss multiple variations of execution. Command line interface arguments are provided so that all the variations can be run through command line arguments.
To focus study regularization, we want to start with a framework, dataset and model that are as familiar and simple as possible.
For a familiar framework, we will pick Tensorflow version 2.3.1. Among frameworks for deep machine learning, Tensorflow is probably the most widely used today.
For a familiar dataset, one of the most well-studied datasets in machine learning is called the MNIST handwritten digits. The MNIST dataset contains 60000 handwritten digits, each 28 pixels on a side, in equal proportion, labeled with their correct interpretation. Here are some less usual examples:

For a simple model, the Tensorflow 2 User Guide section called Writing a training loop from scratch will provide a base model for our analysis. The model predicts MNIST handwritten digit classification using a simple feed forward network.
Our outcome of interest is the level of sparsity our model is achieving. Let's create a measurement to see if our solutions are becoming sparser.
Floating point numbers don't sign up to tell us whether a computed value is equal to another value, only whether the two values are close. So well-posed code for testing must be implemented as for some small .
Tensorflow exposes its model weights in an api called model.trainable_variables, using a class called ResourceVariable. Using these counts of zeros, we can determine model sparsity:
epsilon_zero=0.00001
def count_nonzero_model_weights(model):
vars = {}
numNzTotal = 0
numTotal = 0
for rv in model.trainable_variables:
# rv is a tensorflow.python.ops.resource_variable_ops.ResourceVariable
name = rv.name
num = 0
numNz = 0
for x in np.nditer(rv.value().numpy()):
num += 1
if (abs(x) > epsilon_zero):
numNz += 1
numNzTotal += numNz
numTotal += num
vars[name] = {"num":num, "numNz":numNz}
vars["total"] = {"num":numTotal, "numNz":numNzTotal}
return vars
(Note: repository code contains optimizations to make the code run faster, equivalent to the above.)
Here is an example of what count_nonzero_model will report for sparsity information, in tabular form:
| variable | number of nonzero weights (numNz) | number of weights (num) |
|---|---|---|
| dense_2/kernel:0 | 50169 | 50176 |
| dense_2/bias:0 | 0 | 64 |
| dense_3/kernel:0 | 4096 | 4096 |
| dense_3/bias:0 | 0 | 64 |
| predictions/kernel:0 | 640 | 640 |
| predictions/bias:0 | 0 | 10 |
| total | 54905 | 55050 |
Our quantitative measure of model sparsity will be:
"Regularization" means that we want to change a space of solutions to prefer certain kinds of solutions to others.
For the physics problem "Find all stationary configurations of a rigid planar pendulum subject to the force of gravity", we would immediately notice the solution with the pendulum straight down, depected on the left:
But would we also want the solution with the pendulum straight up, depicted on the right? Here, we could say we prefer stable equilibrium solutions (those where the second derivative of potential energy should be positive), which would be a form of regularization.
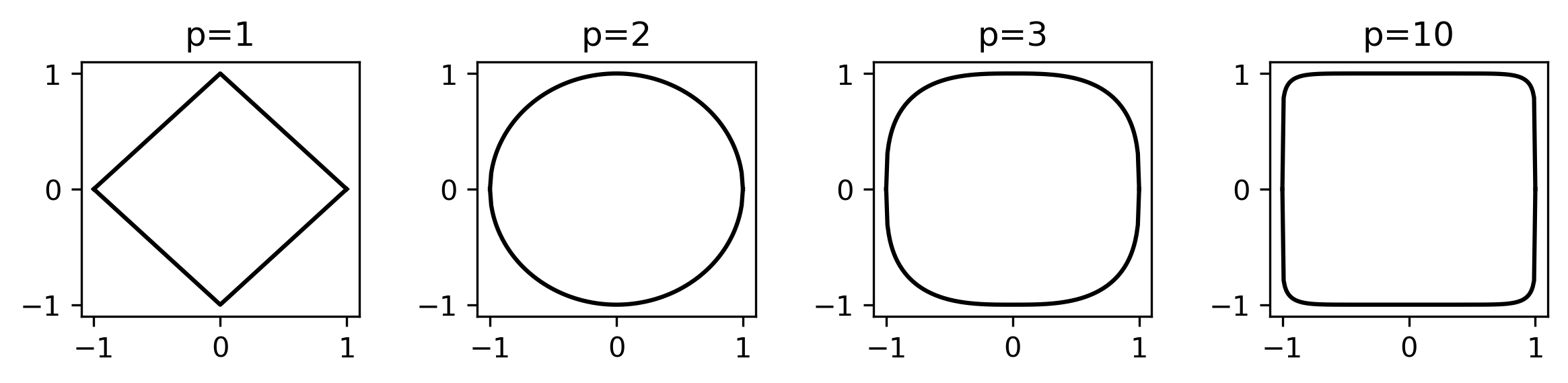
is the name of a way of measuring a distance. is also known as "Manhattan distance", because in two dimensions, it represents the distance a car has to drive between two points if all the roads are on a grid. (Other whole numbers p also have distance measures, called distance.)
Here is a picture of points having an distance of exactly from the origin for a few values of :
In supervised machine learning, we seek to minimize a quantity called the "Risk" (notation and terminology from [Hinton], section 8.1.1):
Since no data set or computing fabric is infinite, we cannot know the risk, so we settle for something called the "Emperical Risk"
and minimize emperical risk by varying . "Training" of our supervised model becomes minimization of emperical risk. Note that in emperical risk, the sum is over each element of training data.
The family of regularizers say that we will not treat all optima of emperical risk equal. Instead, we add to emperical risk a second term that is not a function of the training data, but a function of the parameters . The added term is the distance from the variable parameter vector to the constant parameter vector of all zeros. We multiply the term by one real hyperparameter C.
For , p=1:
In practice, adding the regularization term to our loss function makes sparse solutions more optimal than equivalent dense solutions, but that doesn't mean model training will automatically find zeros.
Let's break into two parts and draw a picture of the problem:
The trouble is that minimizing our emperical risk is a continuous optimization problem. Most continuous optimization algorithms expect to minimize a smooth function.
In fact, the simple base algorithm at the root of most machine learning optimizers is called stochastic gradient descent (SGD). The name describes exactly what it does, descend gradients (also known as derivatives).
For gradents to exist, a function needs to be "smooth" (also known as differentiable). That's the problem. The L1 term is not smooth at the origin:
For each parameter that an ideal optimizer would determine to be zero, the nondifferentiability of the term causes the SGD optimizer to oscillate infinitely around the value of zero for that parameter.
In our training loop, after each epoch, we will call count_nonzero for each layer of our model:
for epoch in range(epochs):
. . .
results_train = model.evaluate(x_train, y_train, verbose=0)
results_test = model.evaluate(x_test, y_test, verbose=0)
nzByVar = count_nonzero_model_weights(model)
print(json.dumps({"event": "measure_test",
"epochAfter": epoch,
"ent_train": results_train[0],
"inacc_train": 1-results_train[1],
"ent_test": results_test[0],
"inacc_test": 1-results_test[1],
"num_nonzero": nzByVar
}),
flush=True)
Tensorflow contains an API for regularization. Most layer creation functions such as layer.Dense
layers.Dense(64, activation="relu")
may be annotated with a parameter for a regularizer:
layers.Dense(64, activation="relu", kernel_regularizer=tf.keras.regularizers.l1(l=c))
Here, the value c is our constant for regularization.
If we run our program, do we get zeros?
python dlregular_tf_fancy.py --numEpochs 200 --regL1Try1 0.0001
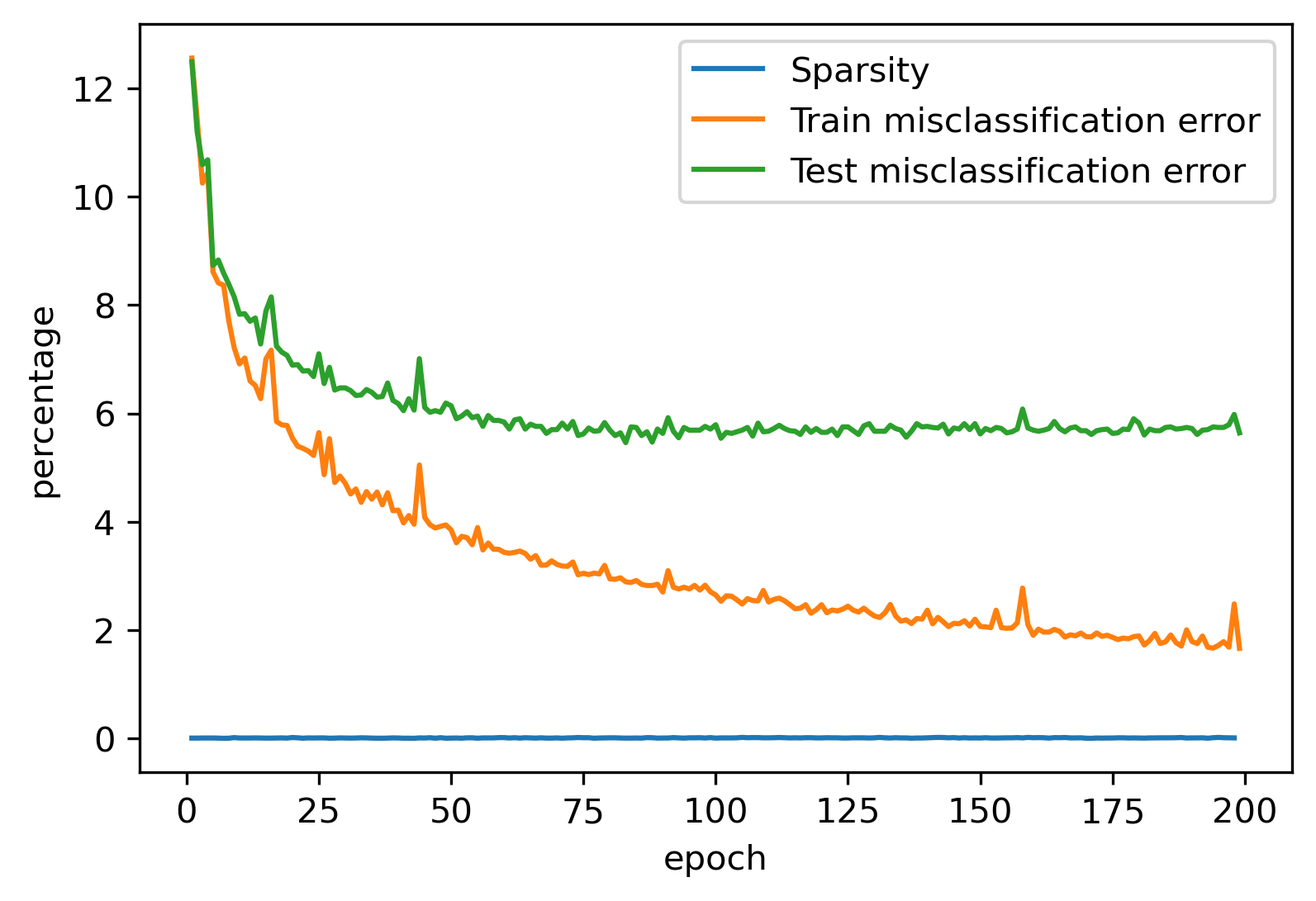
(All measures are percentages.)
The reason we are not finding zeros is that normal SGD-style solvers are designed for optimizing smooth (differentiable) functions. Where each parameter crosses from positive to negative, the absolute value has a nondifferentiability. The nondifferentiability causes SGD search on a parameter that should be zero to oscillate around zero, typically forever.
Tensorflow has another implementation of regularization that offers an instructive comparison. Instead of using our SGD optimizer:
optimizer = keras.optimizers.SGD(learning_rate=learningRate)
we can use an optimizer designed for regularization, the ProximalAdagradOptimizer:
optimizer = tf.compat.v1.train.ProximalAdagradOptimizer(
learningRate,
initial_accumulator_value=learningRate**2,
l1_regularization_strength=cL1)
which is based on the Adagrad optimization algorithm. Adagrad is similar to SGD, but varies the learning rate as the optimizer is training. Adagrad expects a parameter initial_accumulator_value related to learning rate. Changing a learning rate can make a big difference in the behavior of an optimization. Since Adagrad varies learning rate while SGD keeps it constant, we won't be able to make an exact behavioral comparison. To make a best effort to compare apples to apples, we set the value
initial_accumulator_value=learningRate**2
to cause the first step of Adagrad to be the same size that SGD would have taken with the same learningRate.
Note that ProximalAdagradOptimizer only works if we want to apply the same regularization constant to all stages of our model.
Let's try fitting our new model:
python ./dlregular_tf_simple.py --numEpochs 200 --regL1Try2 0.001
Unfortunately, this program will crash:
tensorflow.python.framework.errors_impl.NotFoundError: No registered 'ResourceApplyProximalAdagrad' OpKernel for 'GPU' devices compatible with node {{node ResourceApplyProximalAdagrad}}
due to a bug in Tensorflow 2.3. A workaround for this bug that is sufficent for our purpose is:
try:
# Disable all GPUS
tf.config.set_visible_devices([], 'GPU')
visible_devices = tf.config.get_visible_devices()
for device in visible_devices:
assert device.device_type != 'GPU'
except:
# Invalid device or cannot modify virtual devices once initialized.
pass
Let's try again:
python ./dlregular_tf_simple.py --numEpochs 200 --regL1Try3 0.001
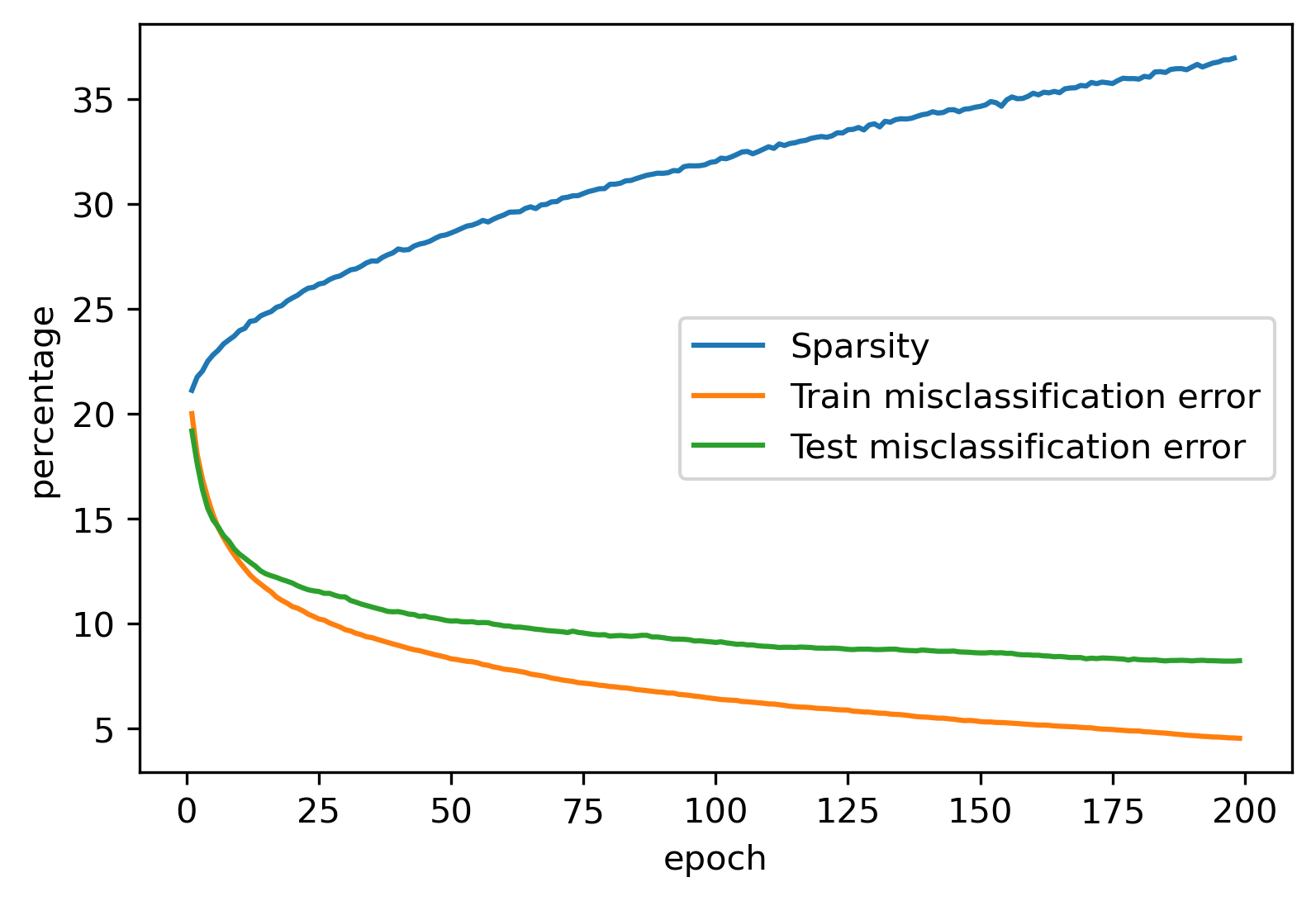
Our model training now succeeds in finding a model with over 35% sparsity. That means your model can now run with 35% less computation. Mission accomplished.
In this article, we saw how deep learning can be guided to find sparse models using a concept from statistical optimization called regularization. Sparse models can make predictions with less hardware.
We showed how to implement an regularized model training using two models provided on Tensorflow 2.3.
While ProximalAdagradOptimizer got us started with sparse models, it left us with some assumptions that are not great for optimizing our sample problem. The Tensorflow 2.3 bug in ProximalAdagradOptimizer forced us to shut off our GPU acceleration, which is a drag for a demonstration model building and a deal breaker for a real-world model building.
In the next article, we will look inside Tensorflow's ProximalAdagradOptimizer and show how we can improve regularization using the good idea of ProximalAdagradOptimizer without its defects.